Poisson disk sampling is an algorithm that generates (fairly) uniform, random points within a domain. It can be used in N dimensions.

Within computational design and additive manufacturing, random points within a 2D or 3D domain are useful because these form seed points for stochastic lattice structures. And we like stochastic lattices for components like bone implants, or conformal lattices within weirdly shaped domains.

This particular algorithm is better than a randomly splattered set of points, because the distance between the points can be controlled by the designer. This will then allow for a more evenly distributed, random lattice structure.

The main steps of the algorithm are as follows:

1. Pick a random starting point in the domain
2. Generate random points a distance between r and 2r away from the starting point
3. For each point, if it is at least a distance of r away from all other points, we add it to our underlying grid.
4. Pick another point in our grid
5. Repeat until we can’t add any more points.

Implementation

The algorithm in this article comes from this paper by Robert Bridson. For simplicity, I’ll implement this as a plugin for Grasshopper in C# so we can visualise the results and watch the algorithm generate in real-time. We need to start by collecting the input parameters:

protected override void RegisterInputParams(GH_Component.GH_InputParamManager pManager)
{
    pManager.AddRectangleParameter("Rectangle", "R", "Rectangle within which to generate points", GH_ParamAccess.item);
    pManager.AddNumberParameter("Distance", "D", "Min point distance", GH_ParamAccess.item);
    pManager.AddIntegerParameter("Seed", "S", "Random seed", GH_ParamAccess.item, 0);
}

I’ll use a Rectangle object to define a 2D region where we will generate the points. This object also contains some useful attributes we will use. We also need to specify the distance, and we will also add an integer seed so we can repeat the process controllably.

Cool, so let’s start writing the SolveInstance method. This is the function that Grasshopper will call to run the algorithm. First, let’s initialise some variables to store our inputs:

protected override void SolveInstance(IGH_DataAccess DA)
{
    // Collect input values
    GH_Number minDistance = new GH_Number();
    if (!DA.GetData("Distance", ref minDistance)) return;

    GH_Rectangle rectangle = new GH_Rectangle();
    if (!DA.GetData("Rectangle", ref rectangle)) return;

    GH_Integer seed = new GH_Integer();
    if (!DA.GetData("Seed", ref seed)) return;
}

We also need to set a few parameters, k, our upper limit on point generation per seed point, and our cellSize. For our cell size, we need the underlying double from our minDistance input value. The cellSize is calulated according to the original paper, ensuring each grid cell can only contain up to a single point:

// Set parameters
int k = 30;
double cellSize = minDistance.Value / Math.Sqrt(2);

The first step in our algorithm is creating a regular grid where we will put our generated points. This is an optimisation made to speed up distance checking. We use the Width and Height attributes of our Rectangle and the cellSize to calculate the number of cells per dimension. I’m also wrapping this in an if statement so that the algorithm only runs if the distance is greater than 0:

if (minDistance.Value > 0) 
{
    int cellsX = (int)Math.Ceiling(rectangle.Value.Width / cellSize);
    int cellsY = (int)Math.Ceiling(rectangle.Value.Height / cellSize);
    int[,] grid = new int[cellsX, cellsY];
...

At this point, we can initialise our list of points, and also an activeList where we keep the points we are working with. We can also initialise our Random object with our seed to generate random double values and int indexes.

List<Point3d> points = new List<Point3d>();
List<Point3d> activeList = new List<Point3d>();

// Initialise Random with seed value
Random random = new Random(seed.Value);

Point3d initialPoint = new Point3d();

Lets assign some random values to our initialPoint and store it in our grid, and lists. We get the grid index, and then store the number 1 in that location to indicate that this is our first point:

initialPoint = new Point3d(
random.NextDouble() * rectangle.Value.Width,
random.NextDouble() * rectangle.Value.Height, 0);

activeList.Add(initialPoint);
points.Add(activeList[0]);

int initialX = (int)Math.Floor(activeList[0].X / cellSize);
int initialY = (int)Math.Floor(activeList[0].Y / cellSize);

grid[initialX, initialY] = 1;

We’re now ready to enter the main while loop of the function. Since we´re going to be adding and removing points from our activeList as we are working, we will use this as our condition to leave the loop. When this list is empty, we’re done. We first choose a random index from our activeList to become the seed point:

while (activeList.Count > 0)
{
    // Get random starting point
    int index = random.Next(activeList.Count);
    Point3d point = activeList[index];
    bool foundValid = false;
...

I’ve also added a boolean value, foundValid, so we know if we’ve generated a valid random point and we can add it to the lists. Within our while loop, we’ll add a for loop to generate up to k random points around our seed point. Instead of just generating some random coordinates, we create a random 3D vector with length between r and 2r, and translate our seed point to generate our new random point:

for (int i = 0; i < k; i++)
{
    // Generate new point from starting point
    double angle = random.NextDouble() * Math.PI * 2;
    Vector3d direction = new Vector3d(Math.Sin(angle), Math.Cos(angle), 0);
    Point3d newPoint = point + direction * minDistance.Value * (1 + random.NextDouble());

We then check to see if this new point is valid, by comparing it to the other points in our grid, using a boolean function IsValid. If our new point is indeed valid, we’ll add it to our lists, and it’s index to our grid, we set foundValid to true, and we break out of the for loop:

    if (IsValid(newPoint, rectangle.Value, cellSize, points, grid))
    {
        points.Add(newPoint);
        activeList.Add(newPoint);
        grid[(int)(newPoint.X / cellSize), (int)(newPoint.Y / cellSize)] = points.Count;
        foundValid = true;
        break;
    }
}
if (!foundValid)
{
    activeList.RemoveAt(index);
}

So all that’s left is to implement the IsValid function. This is where the grid actually comes in really handy. Instead of performing distance checking against every point in our list, we instead figure out which grid cell our new point lies in, and then simply check just the surrounding grid indexes to see if there are any points there. If there are, we check the distance, and if we find one that’s too close, we return false, and the point is discarded. Notice how we use the Width and Height attributes of the Rectangle class to ensure the point is within our specified region first:

protected bool IsValid(Point3d point, Rectangle3d region, double cellSize, List<Point3d> points, int[,] grid)
{
    if (point.X >= 0 && point.X < region.Width && point.Y >= 0 && point.Y < region.Height)
    {
        double minDistance = cellSize * Math.Sqrt(2);
        int cellX = (int)Math.Floor(point.X / cellSize);
        int cellY = (int)Math.Floor(point.Y / cellSize);
        int searchCells = 2;
        int searchStartX = Math.Max(0, cellX - searchCells);
        int searchEndX = Math.Min(cellX + searchCells, grid.GetLength(0) - 1);
        int searchStartY = Math.Max(0, cellY - searchCells);
        int searchEndY = Math.Min(cellY + searchCells, grid.GetLength(1) - 1);

        for (int x = searchStartX; x <= searchEndX; x++)
        {
            for (int y = searchStartY; y <= searchEndY; y++) 
            {
                int pointIndex = grid[x, y] - 1;
                if (pointIndex != -1)
                {
                    Point3d queryPoint = points[pointIndex];
                    double distance = (point - queryPoint).SquareLength;
                    if (distance < minDistance * minDistance)
                    {
                        return false;
                    }
                }
            }
        }
        return true;
    }
    return false;
}

Another optimisation we make here is using the SquareLength instead of the Length. This saves a square root calculation for the distance, and we just need to square the minDistance for comparison.

The only thing left is to convert our list of Point3d objects to GH_Point objects, and output our result to the canvas. We need to add a translationVector to move our points to within our rectangle, since this was not taken into account during point generation:

Vector3d translationVector = new Vector3d(
    rectangle.Value.Center.X - rectangle.Value.Width / 2,
    rectangle.Value.Center.Y - rectangle.Value.Height / 2,
    rectangle.Value.Center.Z);

List<GH_Point> outputList = existingPoints;
    foreach (Point3d point in  points)
    {
        outputList.Add(new GH_Point(point + translationVector));
    }
DA.SetDataList(0, outputList);

Running in Grasshopper

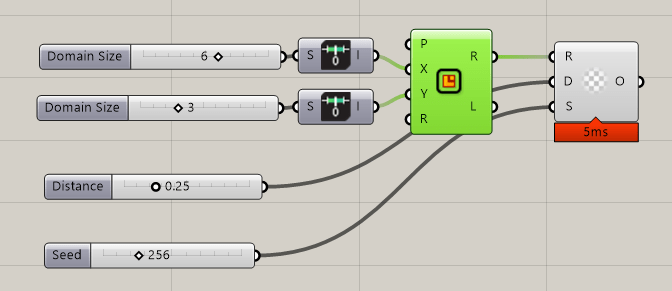
Once this code is compiled, we can drag the component onto the canvas, create our bounding rectangle and connect sliders for the point distance, and seed values. This will give us an instant preview of our nicely distributed points.

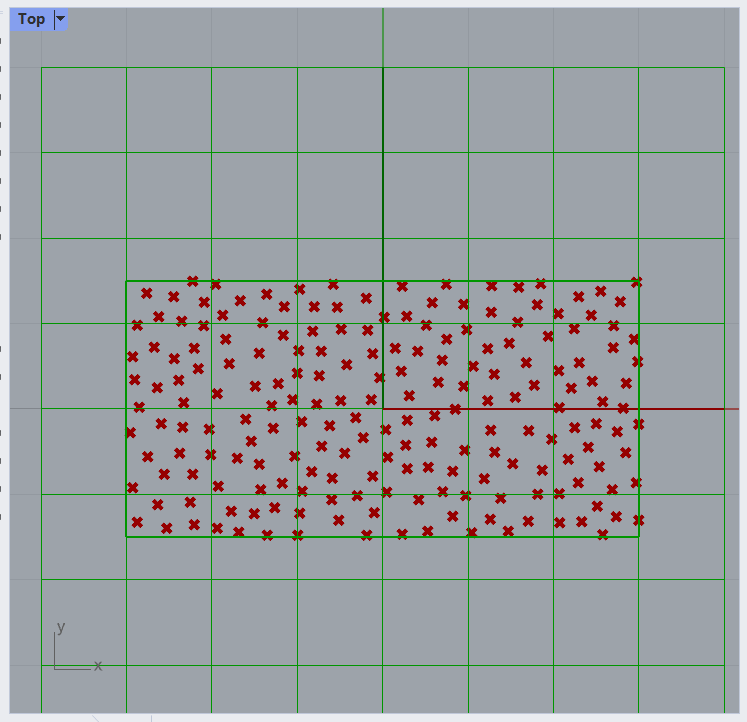
If we want to, we can then use these to create a delauney triangulation, or even a voronoi pattern:

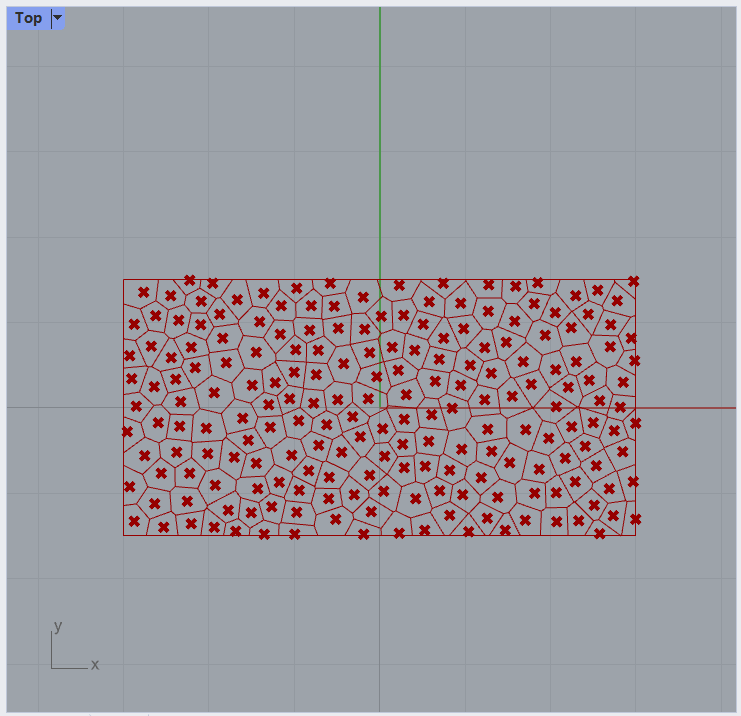
We see fairly evenly-sized voronoi cells, and we have some control over this size.

Using a preexisting points list

For some use cases, we may want even more control by either being able to choose the initial seed location, or have a pre-existing list of points we want to fill around with random points. This is a pretty easy extension to add to the code we already have.

First, we add an input value to accept this point list, and make it an optional parameter:

protected override void RegisterInputParams(GH_Component.GH_InputParamManager pManager)
{
    pManager.AddRectangleParameter("Rectangle", "R", "Rectangle within which to generate points", GH_ParamAccess.item);
    
    // Add in our existing points
    pManager.AddPointParameter("Existing Points", "P", "Optional list of pre-existing points to include in the set", GH_ParamAccess.list);
    pManager[1].Optional = true;

    pManager.AddNumberParameter("Distance", "D", "Min point distance", GH_ParamAccess.item);
    pManager.AddIntegerParameter("Seed", "S", "Random seed", GH_ParamAccess.item, 0);
}

Inside the SolveInstance method, we create a new list to store our pre-existing points:

List<GH_Point> existingPoints = new List<GH_Point>();
DA.GetDataList("Existing Points", existingPoints);

Remember how our random point generation doesn’t take the Rectangle position into account until the end? Well, our pre-existing points will, so these need to be translated using our translationVector. These will also be added immediately to our existingPointList:

List<Point3d> existingPointList = new List<Point3d>(existingPoints.Count);
foreach(GH_Point p in existingPoints)
{
    existingPointList.Add(p.Value - translationVector);
}

At this point, I chose to use the first point in our existingPoints list as the initial point. This allows us to choose the initial seed:

if (existingPointList.Count > 0 ){    initialPoint = existingPointList[random.Next(0, existingPointList.Count - 1)];}else{    initialPoint = new Point3d(    random.NextDouble() * rectangle.Value.Width,    random.NextDouble() * rectangle.Value.Height, 0);}

We now need to update our IsValid function to include our pre-existing points. For simplicity, I decided not to include these into our grid search. The reasons for this are 1) because this list probably won’t be too long and the added time would be negligible, and 2) these points may not obey our minimum distance criteria, so wouldn’t fit 1 per grid cell.

We update the signature of IsValid to include the existingPoints, and add in the distance checking:

if (existingPoints.Count > 0)
{
    foreach (Point3d existingPoint in existingPoints)
    {
        double existingDistance = (point - existingPoint).SquareLength;
        if (existingDistance < minDistance * minDistance)
        {
            return false; 
        }
    }
}

This new addition means we can do some fun things:

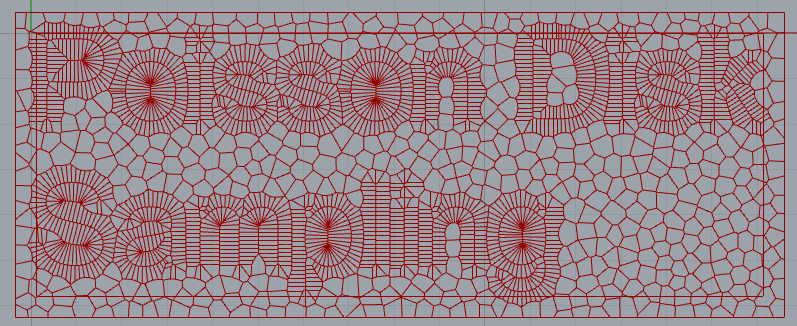
Summary

In this article, I have described the implementation of a component for Grasshopper in C# that uses Poisson Disk sampling to create random points within a rectangular domain that are evenly spaced, controlled by a distance parameter. This particular implementation uses a grid search to improve the speed of the algorithm. It has a time complexity of O(N), so it scales well for large point sets. I then extended this base implementation to include a list of pre-existing points, giving us some more control.

There are a load of optimisations we could make to this code, but for now it’s fast enough.

Check out Part 2 where I move this into 3D and create lattice structures!

Thanks for reading!